| Re: Teaching Seen as Crucial in Topping Education Rankings (754329) | |||
|
|
|||
| Home > OTChat | |||
|
[ Read Responses | Post a New Response | Return to the Index ] |
|
||
Re: Teaching Seen as Crucial in Topping Education Rankings |
|
|
Posted by JayMan on Sat Mar 19 11:26:53 2011, in response to Re: Teaching Seen as Crucial in Topping Education Rankings, posted by cortelyounext on Fri Mar 18 13:40:34 2011. The standard deviation is a measure of the variability of whatever you're dealing with. It's basically how spread out your data points are. It's expressed in the units of what you're measuring. Data with a low standard deviation tend to be tightly clustered around the mean (the average), whereas those with a higher standard deviation are all over the place. The standard deviation of height, for example, is much lower on a basketball team (where most of the players are tall) than it is in the general population.When things are normally distributed (i.e., a bell curve), the mean and the standard deviation define the size and shape of the curve: 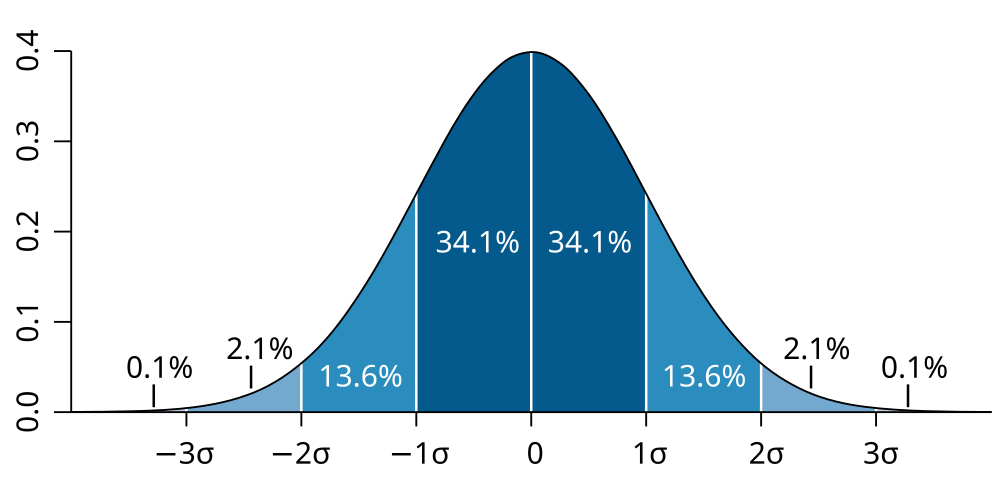 Each standard deviation (σ) is marked. When it comes to IQ, IQ tests are scored such that the mean of the score is set to 100 and the standard deviation is 15 (among whites, at least). As such, a person with an IQ of 115 is 1σ above the mean, and outscores 84% of the (white) population. A person with an IQ of 145 (3σ), outscores 99.9% of the (white) population. As we seen, different racial groups have different means, but some groups may even have different standard deviations: India for example has a mean IQ of about 87, (not much different from the black American mean), but we all know a lot of smart Indians -- it is possible that standard deviation of India is much higher than most places, owing to centuries of invasions and migration and endogamous mating (i.e., partial inbreeding) in some places. |